💡 Takeaway:
The conditional autoencoder captures more return variation and risk pricing than traditional models. It excels at return prediction and generates low pricing errors without violating no-arbitrage.
Key Idea: What Is This Paper About?
Gu, Kelly, and Xiu introduce an autoencoder-based asset pricing model that learns nonlinear relationships between firm characteristics and latent factor exposures. This deep learning framework embeds no-arbitrage constraints, making it a valid stochastic discount factor (SDF) model. It beats both linear conditional models (like IPCA) and observable factor models (like Fama-French) in out-of-sample prediction and pricing error minimization.
Economic Rationale: Why Should This Work?
📌 Relevant Economic Theories and Justifications:
- Nonlinear Risk Exposures: True return drivers likely interact with characteristics in nonlinear ways.
- No-Arbitrage Pricing Kernel: The model builds an SDF from latent factors, enforcing pricing consistency.
- Managed Portfolios as Factors: Inputs are built from characteristic-sorted portfolios, connecting to modern factor theory.
- Information Efficiency: The model captures more subtle cross-sectional variation using deep neural networks.
📌 Why It Matters:
This model aligns ML with economic structure—capturing return predictability without alpha. It also helps identify whether return signals stem from risk premia or mispricing.
Data, Model, and Strategy Implementation
Data Used
- Period: 1957–2016 (CRSP monthly stocks)
- Assets: ~30,000 stocks, 6,200 average per month
- Characteristics: 94 firm-level signals (value, momentum, volatility, etc.)
- Benchmarks: FF3–FF6, PCA, IPCA
Model / Methodology
- Model: Conditional Autoencoder (CA0–CA3), increasing depth
- Factor Inputs: Managed portfolios (characteristic-sorted returns)
- Architecture:
- Beta network: multi-layer NN from firm characteristics
- Factor network: linear compression of managed portfolios
- Training: 18-year rolling windows with early stopping and L1 regularization
- Evaluation: Out-of-sample R² and Sharpe ratios over 1987–2016
Trading Strategy (Long-Short Portfolios)
- Signal: Rank stocks by predicted returns
- Portfolio: Long top decile, short bottom decile
- Weighting: Equal-weighted and value-weighted versions
- Rebalance: Monthly
- Sharpe Ratios:
- CA2 Equal-Weight: 2.63
- CA2 Value-Weight: 1.53
- No-Arbitrage: Model has no intercept; all alpha must come from risk pricing
Key Table or Figure from the Paper
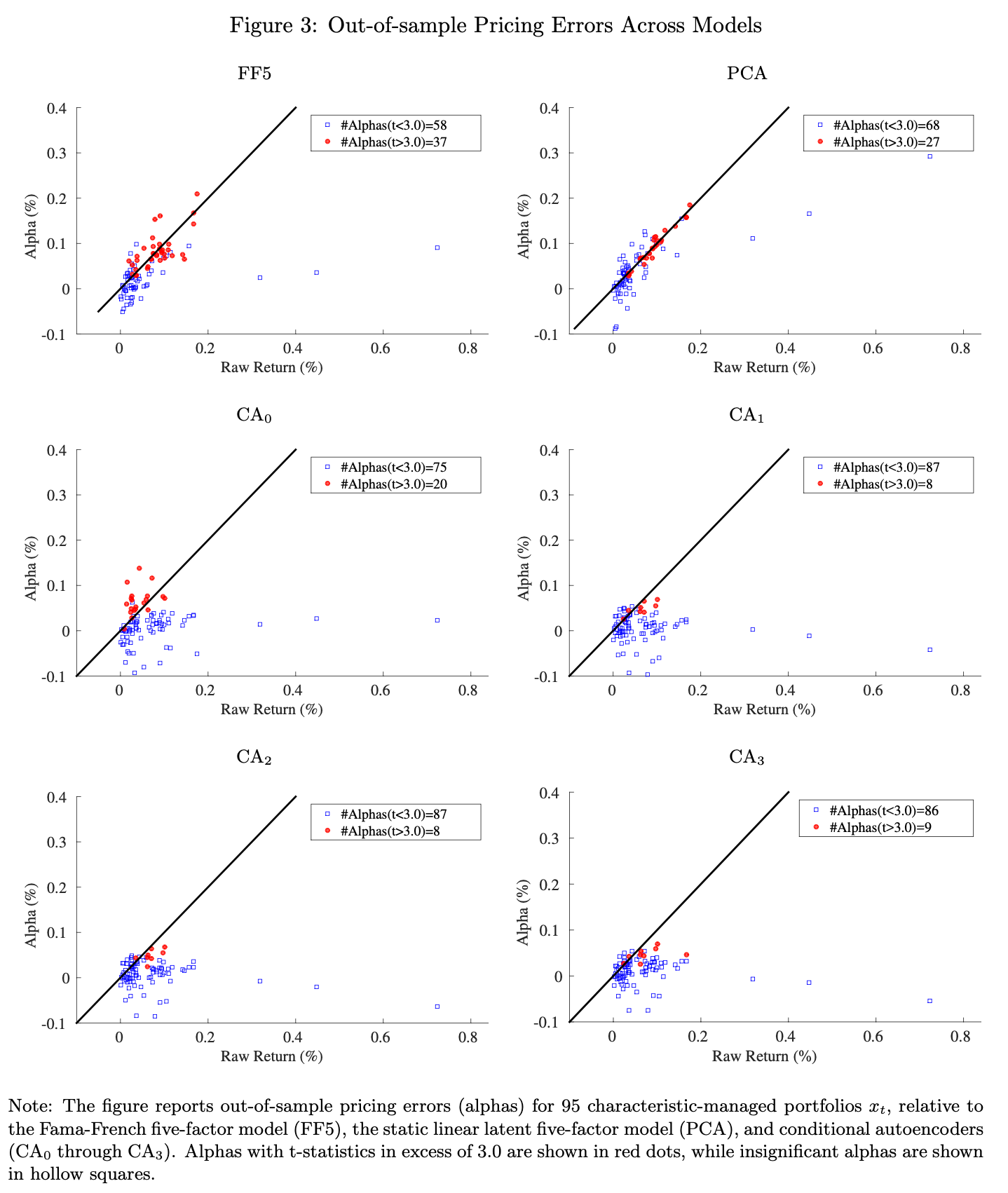
📊 Reference: [Figure 3] – Out-of-Sample Pricing Errors (Alphas) Across Models
📌 Explanation:
- Compares alpha (pricing error) distributions across models.
- Fama-French: 37 portfolios with t-stat > 3.0
- Autoencoder CA2: Only 8 significant alphas—all small
- Shows CA2 better satisfies no-arbitrage pricing
- Demonstrates model’s success in explaining return variation via risk, not mispricing
Final Thought
💡 Deep learning meets no-arbitrage: the future of asset pricing is both flexible and disciplined. 🧠📈
Paper Details (For Further Reading)
- Title: Autoencoder Asset Pricing Models
- Authors: Shihao Gu, Bryan Kelly, Dacheng Xiu
- Publication Year: 2019
- Journal/Source: Working Paper (Booth, Yale, AQR)
- Link: https://ssrn.com/abstract=3335536
